Do We Need To Calculate Register File Twice For R Type?

T-Test Essentials: Definition, Formula and Calculation

How To Do Ii-Sample T-test in R

This commodity describes how to exercise a two-sample t-exam in R (or in Rstudio). Note the two-sample t-test is also referred as:

contained t-test,
contained samples t-test,
unpaired t-test or
unrelated t-test.

The contained samples t-exam comes in two different forms:

the standard Student'southward t-test, which assumes that the variance of the 2 groups are equal.
the Welch's t-test, which is less restrictive compared to the original Student's test. This is the test where you do not presume that the variance is the same in the 2 groups, which results in the fractional degrees of freedom.

The two methods requite very similar results unless both the group sizes and the standard deviations are very different.

You lot will learn how to:

Perform the independent t-test in R using the following functions :
- t_test() [rstatix packet]: the result is a data frame for easy plotting using the ggpubr package.
- t.examination() [stats packet]: R base of operations part.
Interpret and report the 2-sample t-test
Add p-values and significance levels to a plot
Summate and report the independent samples t-test consequence size using Cohen'south d. The d statistic redefines the difference in means as the number of standard deviations that separates those means. T-test conventional issue sizes, proposed by Cohen, are: 0.2 (pocket-size effect), 0.5 (moderate effect) and 0.8 (big effect) (Cohen 1998).

Contents:

Prerequisites
Demo data
Summary statistics
Calculation
- Using the R base role
- Using the rstatix package
Interpretation
Issue size
- Cohen's d for Pupil t-test
- Cohen'south d for Welch t-exam
Study
Summary
References

Related Book

Practical Statistics in R 2 - Comparing Groups: Numerical Variables

Prerequisites

Brand certain you have installed the following R packages:

tidyverse for data manipulation and visualization
ggpubr for creating easily publication ready plots
rstatix provides piping-friendly R functions for piece of cake statistical analyses.
datarium: contains required data sets for this chapter.

Offset by loading the post-obit required packages:

                    library(tidyverse) library(ggpubr) library(rstatix)

Demo data

Demo dataset: genderweight [in datarium package] containing the weight of twoscore individuals (20 women and twenty men).

Load the data and show some random rows by groups:

                    # Load the data data("genderweight", packet = "datarium") # Show a sample of the data past group set.seed(123) genderweight %>% sample_n_by(group, size = ii)

                    ## # A tibble: 4 x 3 ##   id    group weight ##   <fct> <fct>  <dbl> ## 1 half-dozen     F       65.0 ## 2 15    F       65.9 ## 3 29    M       88.nine ## four 37    One thousand       77.0

We want to know, whether the average weights are dissimilar betwixt groups.

Summary statistics

Compute some summary statistics by groups: mean and sd (standard difference)

                    genderweight %>%   group_by(group) %>%   get_summary_stats(weight, type = "mean_sd")

                    ## # A tibble: 2 x 5 ##   grouping variable     north  mean    sd ##   <fct> <chr>    <dbl> <dbl> <dbl> ## 1 F     weight      xx  63.5  2.03 ## 2 G     weight      20  85.8  4.35

Calculation

Call back that, by default, R computes the Welch t-test, which is the safer one. This is the exam where you do non assume that the variance is the same in the two groups, which results in the fractional degrees of freedom. If you lot want to presume the equality of variances (Student t-test), specify the option var.equal = True.

Using the R base of operations function

There are two options for calculating the contained t-examination depending whether the two groups information are saved either in two different vectors or in a information frame.

Option i. The information are saved in ii different numeric vectors:

                      # Save the data in 2 unlike vector women_weight <- genderweight %>%   filter(group == "F") %>%   pull(weight) men_weight <- genderweight %>%   filter(group == "M") %>%   pull(weight) # Compute t-examination res <- t.exam(women_weight, men_weight) res

                      ##  ##  Welch Two Sample t-test ##  ## data:  women_weight and men_weight ## t = -xx, df = thirty, p-value <2e-xvi ## culling hypothesis: true deviation in means is non equal to 0 ## 95 percent confidence interval: ##  -24.5 -20.1 ## sample estimates: ## mean of 10 mean of y  ##      63.5      85.8

Option two. The data are saved in a data frame.

                      # Compute t-test res <- t.examination(weight ~ group, information = genderweight) res

                      ##  ##  Welch Two Sample t-test ##  ## data:  weight by grouping ## t = -20, df = 30, p-value <2e-sixteen ## alternative hypothesis: truthful divergence in means is not equal to 0 ## 95 percentage confidence interval: ##  -24.v -20.1 ## sample estimates: ## mean in group F hateful in group M  ##            63.5            85.8

As you can see, the ii methods requite the same results.

In the result above :

t is the t-examination statistic value (t = -20.79),
df is the degrees of freedom (df= 26.872),
p-value is the significance level of the t-exam (p-value = 4.29810^{-18}).
conf.int is the conviction interval of the ways difference at 95% (conf.int = [-24.5314, -20.1235]);
sample estimates is the hateful value of the sample (mean = 63.499, 85.826).

Using the rstatix bundle

Nosotros'll apply the pipage-friendly t_test() function [rstatix package], a wrapper around the R base office t.test(). The results tin can be easily added to a plot using the ggpubr R package.

                      stat.test <- genderweight %>%    t_test(weight ~ group) %>%   add_significance() stat.exam

                      ## # A tibble: i x 9 ##   .y.    group1 group2    n1    n2 statistic    df        p p.signif ##   <chr>  <chr>  <chr>  <int> <int>     <dbl> <dbl>    <dbl> <chr>    ## 1 weight F      M         20    20     -xx.eight  26.9 4.30e-eighteen ****

If you want to assume the equality of variances (Educatee t-test), specify the choice var.equal = Truthful:

                      stat.test2 <- genderweight %>%   t_test(weight ~ grouping, var.equal = True) %>%   add_significance() stat.test2

The results above show the following components:

.y.: the y variable used in the test.
group1,group2: the compared groups in the pairwise tests.
statistic: Test statistic used to compute the p-value.
df: degrees of freedom.
p: p-value.

Note that, you tin obtain a detailed result past specifying the option detailed = TRUE.

                      genderweight %>%   t_test(weight ~ grouping, detailed = TRUE) %>%   add_significance()

                      ## # A tibble: 1 x xvi ##   estimate estimate1 estimate2 .y.    group1 group2    n1    n2 statistic        p    df conf.depression conf.high method culling p.signif ##      <dbl>     <dbl>     <dbl> <chr>  <chr>  <chr>  <int> <int>     <dbl>    <dbl> <dbl>    <dbl>     <dbl> <chr>  <chr>       <chr>    ## ane    -22.3      63.five      85.8 weight F      M         20    20     -20.8 4.30e-18  26.9    -24.5     -20.1 T-test two.sided   ****

Estimation

The p-value of the test is 4.310^{-xviii}, which is less than the significance level alpha = 0.05. We tin conclude that men'south average weight is significantly different from women'due south average weight with a p-value = iv.310^{-18}.

Consequence size

Cohen'south d for Pupil t-test

There are multiple version of Cohen'south d for Pupil t-exam. The virtually unremarkably used version of the Student t-test result size, comparing two groups (\(A\) and \(B\)), is calculated by dividing the mean deviation between the groups by the pooled standard deviation.

Cohen's d formula:

\[
d = \frac{m_A - m_B}{SD_{pooled}}
\]

where,

\(m_A\) and \(m_B\) represent the mean value of the grouping A and B, respectively.
\(n_A\) and \(n_B\) represent the sizes of the grouping A and B, respectively.
\(SD_{pooled}\) is an estimator of the pooled standard difference of the ii groups. Information technology can be calculated as follow :
\[
SD_{pooled} = \sqrt{\frac{\sum{(x-m_A)^2}+\sum{(x-m_B)^2}}{n_A+n_B-2}}
\]

Adding. If the selection var.equal = True, then the pooled SD is used when compting the Cohen's d.

                      genderweight %>%  cohens_d(weight ~ group, var.equal = TRUE)

                      ## # A tibble: 1 x 7 ##   .y.    group1 group2 effsize    n1    n2 magnitude ## * <chr>  <chr>  <chr>    <dbl> <int> <int> <ord>     ## 1 weight F      G        -6.57    xx    20 big

At that place is a big effect size, d = six.57.

Annotation that, for small sample size (< 50), the Cohen's d tends to over-inflate results. There exists a Hedge's Corrected version of the Cohen's d (Hedges and Olkin 1985), which reduces effect sizes for small samples past a few percentage points. The correction is introduced by multiplying the usual value of d by (N-three)/(N-2.25) (for unpaired t-test) and by (n1-2)/(n1-i.25) for paired t-exam; where N is the full size of the ii groups being compared (N = n1 + n2).

Cohen'south d for Welch t-exam

The Welch test is a variant of t-exam used when the equality of variance can't be assumed. The consequence size can be computed by dividing the mean difference between the groups by the "averaged" standard deviation.

Cohen'south d formula:

\[
d = \frac{m_A - m_B}{\sqrt{(Var_1 + Var_2)/2}}
\]

where,

\(m_A\) and \(m_B\) represent the hateful value of the grouping A and B, respectively.
\(Var_1\) and \(Var_2\) are the variance of the ii groups.

Calculation:

                      genderweight %>% cohens_d(weight ~ grouping, var.equal = FALSE)

                      ## # A tibble: 1 ten 7 ##   .y.    group1 group2 effsize    n1    n2 magnitude ## * <chr>  <chr>  <chr>    <dbl> <int> <int> <ord>     ## ane weight F      Thou        -6.57    twenty    20 large

Note that, when group sizes are equal and grouping variances are homogeneous, Cohen's d for the standard Educatee and Welch t-tests are identical.

Study

We could report the result as follow:

The mean weight in female person grouping was 63.v (SD = two.03), whereas the mean in male group was 85.viii (SD = four.3). A Welch two-samples t-exam showed that the divergence was statistically pregnant, t(26.9) = -xx.eight, p < 0.0001, d = 6.57; where, t(26.9) is shorthand annotation for a Welch t-statistic that has 26.9 degrees of liberty.

Visualize the results:

                    # Create a box-plot bxp <- ggboxplot(   genderweight, x = "group", y = "weight",    ylab = "Weight", xlab = "Groups", add = "jitter"   )  # Add p-value and significance levels stat.examination <- stat.exam %>% add_xy_position(ten = "group") bxp +    stat_pvalue_manual(stat.test, tip.length = 0) +   labs(subtitle = get_test_label(stat.examination, detailed = TRUE))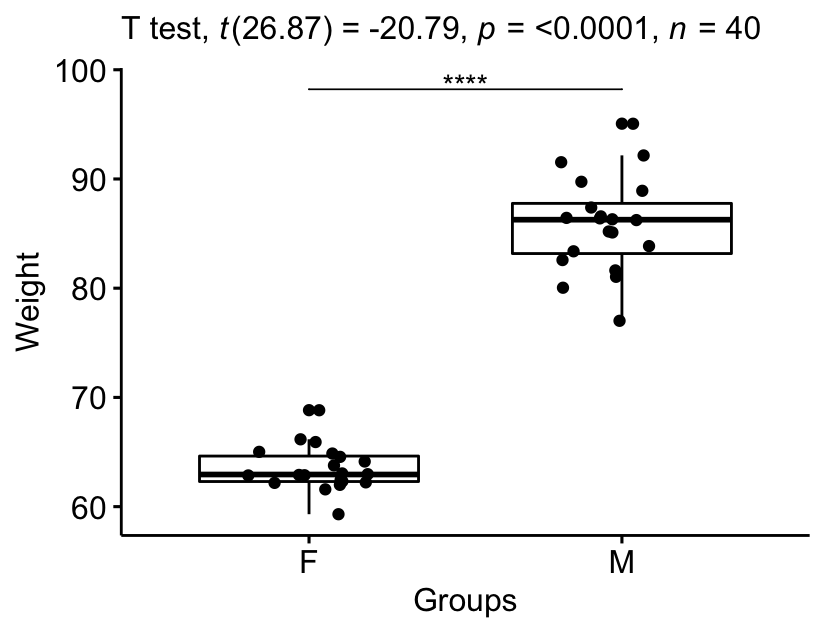

Summary

This article shows how to perform the 2-sample t-test in R/Rstudio using two different means: the R base function t.test() and the t_test() function in the rstatix package. We also describe how to interpret and written report the t-examination results.

References

Cohen, J. 1998. Statistical Ability Analysis for the Behavioral Sciences. 2nd ed. Hillsdale, NJ: Lawrence Erlbaum Associates.

Hedges, Larry, and Ingram Olkin. 1985. "Statistical Methods in Meta-Assay." In Stat Med. Vol. xx. doi:x.2307/1164953.

Recommended for you

This section contains all-time data science and self-development resource to assistance y'all on your path.

Version: Français

Back to T-Test Essentials: Definition, Formula and Calculation